Модель спроса и предложения для цены биткойна

В этой статье автор пытается смоделировать цену биткойна как функцию от спроса и предложения. Он исследует возможность использования двойной логарифмической временной модели для спроса и предложения и отвергает её по причине серьёзной гетероскедастичности. Затем с помощью программы auto.arima, он находит достаточно производительную модель авторегрессионного интегрированного скользящего среднего. После этого он использует построенный с помощью ARIMA прогноз спроса и предложения при моделировании будущей цены биткойна, с учётом того, что объём его предложения заведомо известен.

Примечания

• Минимально необходимое предварительное чтение:
  • https://bitnovosti.com/2019/04/03/modelirovanie-tseny-bitkojna-ishodya-iz-ego-defitsitnosti/
  • https://bitnovosti.com/2019/09/27/falsifitsirovanie-koeffitsienta-stock-to-flow-kak-modeli-stoimosti-bitkojna/
  • https://ru.wikipedia.org/wiki/Закон_спроса_и_предложения
• Анализ был выполнен с помощью Stata 14 and R 3.4.4
• Не является финансовой рекомендацией.
• Все модели неверны, но некоторые из них полезны.

Введение

Отношение запасов к приросту (Stock to Flow), обозначение которого здесь мы для удобства сократим до St/F, как было доказано (1, 2), является неложным предиктором цены биткойна.

Распространённая критика моделирования цены с помощью St/F заключается в том, что при этом не учитывается влияние спроса. В конце концов, ведь цена является функцией от объёма предложения и спроса. В St/F моделируется предложение, но как построенные на основе этой метрики модели реагируют на изменение спроса?

В рамках этой статьи мы примем за абсолютную истину две идеи, даже при том, что они могут таковыми не оказаться. Мы будем называть эти истины аксиомами, и мы сформулируем эти аксиомы так, чтобы установить некую основу, исходя из которой можно будет развивать модель спроса и предложения.

Условные обозначения

Традиционно расчётное значение статистического параметра обозначается «шапкой» над символом. Здесь вместо него мы будем использовать [ ], т.е. расчётное значение β = [β]. Матрицу 2×2 мы будем представлять как [r1c1, r1c2 \ r2c1, r2c2] и т.д. Для обозначения индексированных элементов будем использовать символ @ – например, для 10-й позиции в векторе X обычно используется X с подстрочным индексом 10. Вместо этого, мы будем писать X@10.

Аксиома 1: Цена является функцией от спроса и предложения

Цитируя англоязычную Wiki,

В микроэкономике спрос и предложение являются экономической моделью рыночного ценообразования. Постулируется, что, при прочих равных, на конкурентном рынке цена за единицу определённого товара или другого объекта торговли, такого как рабочая сила или ликвидные финансовые активы, будет изменяться пока не придёт к точке, в которой спрос (для текущей цены) сравняется с предложением (по текущей цене) и не установится экономическое равновесие.

Предположим, что: цена (P) = спрос (D) / предложение (S). Рост предложения при неизменном уровне спроса приводит к снижению цены. Рост спроса D при неизменном уровне предложения приводит к росту цены.

Здесь мы определяем прирост количества актива (flow в коэффициенте St/F) как месячный прирост, чтобы избежать путаницы с долгосрочными эффектами. Теперь давайте предположим, что сторона предложения биткойна моделируется от обратного по отношению к дефицитности (т.е. от изобилия), то есть S= 1/St/F +ε = F/St+ε, где ε – это некоторая произвольная погрешность. Наше уравнение для цены в этом случае будет выглядеть так: P= D/(F/St+ε). Предположим также, что спрос D тоже является некоторой производной. И предположим, что ε является независимым и случайно распределённым значением, со среднеарифметическим около 0,1, и, следовательно, его можно (пока) проигнорировать в модели.

Тогда мы получаем, что P = D/(F/St), из чего следует, что D = PF/St.

Аксиома 2: Спрос является функцией от времени t

Добавим условие о том, что спрос моделируется некоторой функцией времени f(t)=D=βt.

Регрессия обычных наименьших квадратов (OLS) – это метод нахождения линейной зависимости между двумя и более переменными. Для начала давайте определим линейную модель как некоторую функцию X, которая равна Y с некоторой погрешностью:

Y = βX+ε

где Y – зависимая переменная, X – независимая переменная, ε – это величина погрешности, а β – множитель X. Задача OLS – вывести значение β так, чтобы минимизировать ε.

Для того чтобы вывести надёжное расчётное значение [β], необходимо соблюсти некоторые основные условия:

Наличие линейной связи между зависимой и независимой переменными

Гомоскедастичность (то есть постоянство дисперсии) погрешностей

Среднее значение распределения погрешностей обычно равно нулю

Отсутствие автокорреляции ошибок (то есть они не коррелируют с последовательностью ошибок, взятых со сдвигом по времени)

Теперь мы можем рассчитать [D] с помощью модели наименьших квадратов [D]=[β]t+ε.

Линейность

Для начала взглянем на неизменённую диаграмму рассеяния для отношения спроса ко времени.

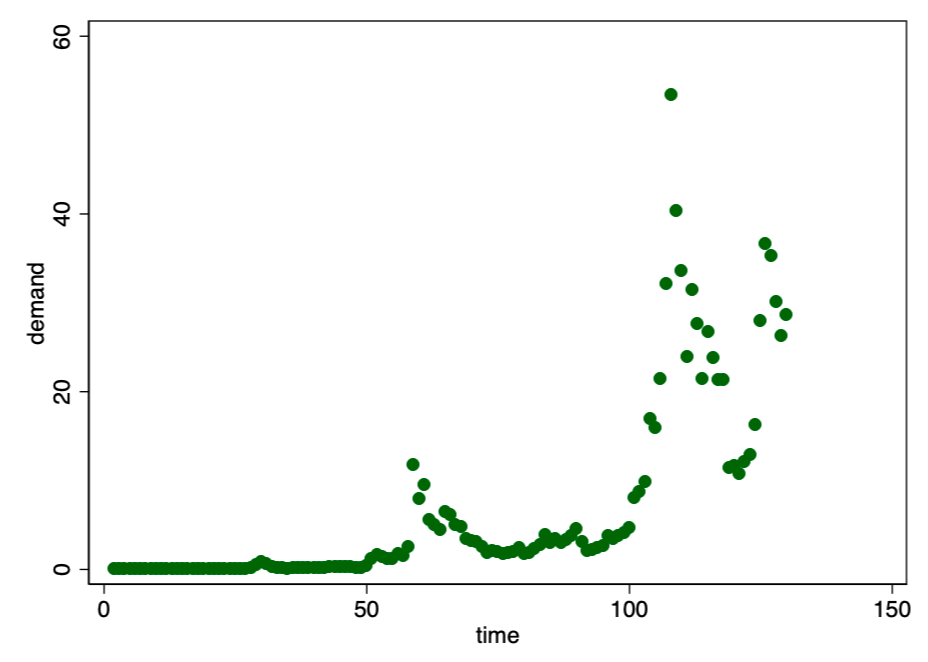Рисунок 1. Отношение спроса ко времени выглядит как потенциально экспоненциальное.

На рисунке 1 мы видим знакомый уже паттерн экспоненциального роста. Для таких случаев, как правило, хорошо подходит двойная логарифмическая модель (рисунок 2).

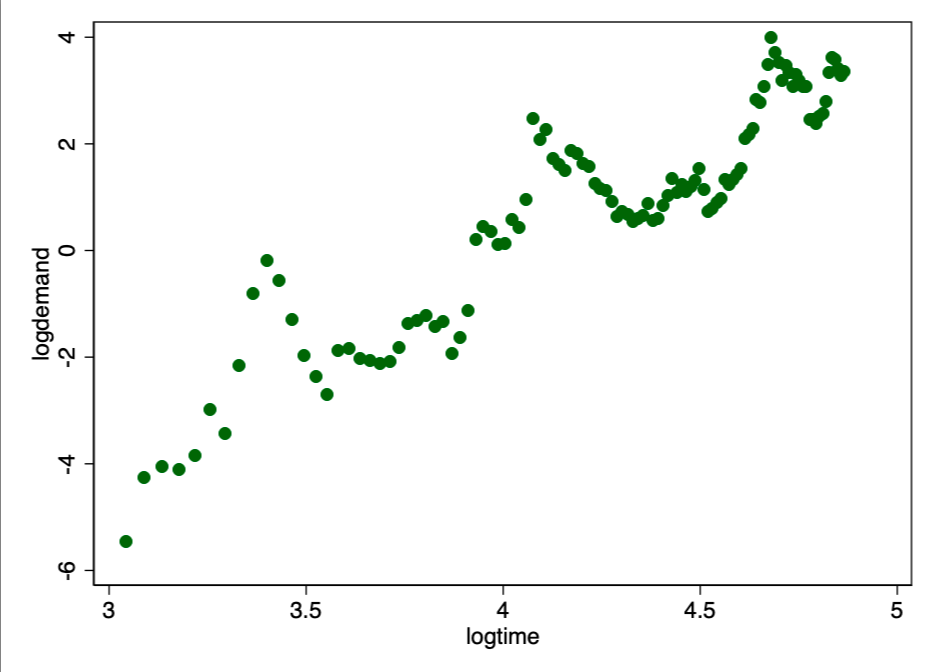Рисунок 2. Прямая линия на двойном логарифмическом графике указывает на хорошее соответствие для экспоненциального отношения. 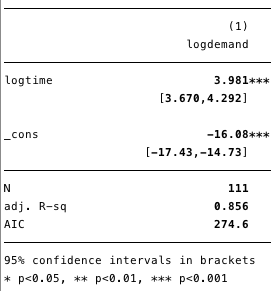Рисунок 3. Бутстрапированная двойная логарифмическая регрессия (с использованием робастной оценки для дисперсии)

Как показано на рисунке 3, наше расчётное значение равно log([D])=3,98log(t) -16, из чего мы можем заключить, что для каждого 10% увеличения во времени мы ожидаем увеличения спроса на 46% (напр. 1,10^3,98=1,46).

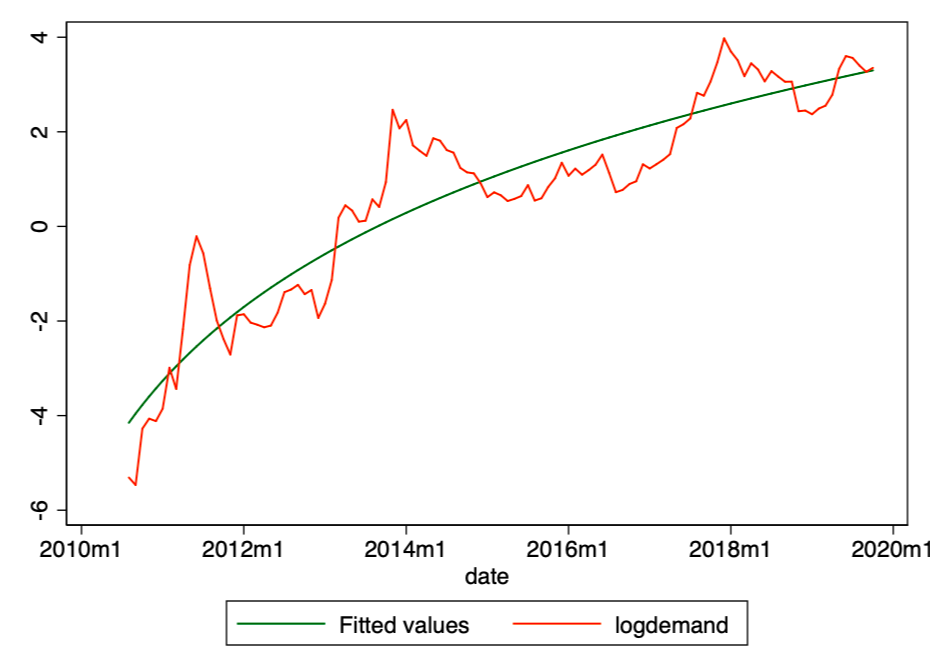Рисунок 4. Расчётные значения (зелёная линия) и фактические логарифмические значения спроса (красная линия).

Используя эту модель, мы теперь можем определить остатки [ε] и расчётные значения [Y], а также проверить соответствие другим условиям.

Гомоскедастичность

При соблюдении условия о постоянстве дисперсии в величине погрешности (т.е. о гомоскедастичности), погрешность для каждого значения прогнозируемой стоимости колеблется произвольным образом около нуля. Следовательно, график отношения остаточной стоимости к расчётной (рис. 5) представляет собой простой и эффективный способ графически проверить выполнение этого условия. На рисунке 5 мы наблюдаем определённый паттерн, а не случайное рассеяние, что указывает на значительное непостоянство дисперсии в величине погрешности (т.е. на гетероскедастичность).

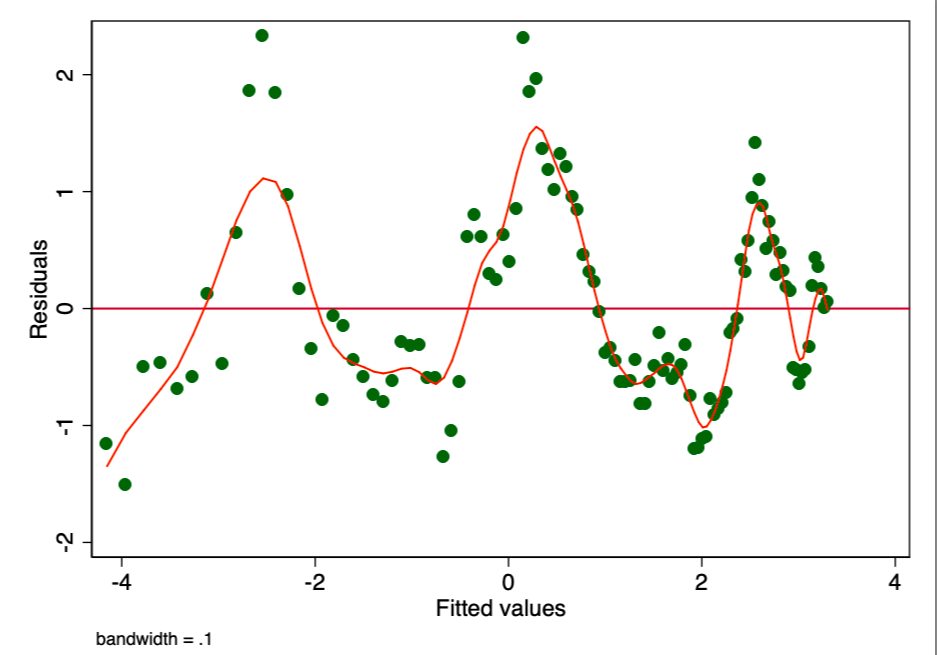Рисунок 5. График отношения остаточной стоимости к расчётной. Наличие паттерна указывает на возможную проблему.

Следствием подобной гетероскедастичности является намного бóльшая дисперсия и, соответственно, меньшая точность расчётных значений коэффициентов [β]. Кроме того, она приводит к преувеличенной значимости p-значений, поскольку метод OLS не выявляет повышенную дисперсию. Поэтому для расчёта t- и F-величин мы используем заниженное значение дисперсии, приводящее к более высокой (недостоверной) значимости. Это влияет также на 95% доверительный интервал для [β], который тоже является функцией дисперсии (через стандартную погрешность). Чтобы попытаться улучшить эту ситуацию, мы использовали для определения величины дисперсии и бутстрапирования (это форма повторной выборки) регрессии робастную «сэндвич»-оценку (оценку Хубера). Однако эти результаты указывают, что даже после всех сделанных корректировок мы по-прежнему не можем доверять результатам этого взятия обычных наименьших квадратов. Можно сказать, что этой проблеме подвержена каждая OLS-модель времени и цены (как, например, приведённая здесь). Поэтому вместо неё мы будем исследовать другую, более подходящую модель времени – модель ARIMA.

ARIMA

Более подходящий, чем простая регрессия времени или её вариации, ARIMA – это метод, разработанный для моделирования изменений временных рядов с течением времени. ARIMA – это сокращение от Auto Regressive Integrated Moving Averages, что переводится как «авторегрессионные интегрированные скользящие средние». Этот метод включает в себя целый класс моделей, которые объясняют временные ряды на основе их собственных прошлых значений – таких, как лаги или отображаемые с запаздыванием ошибки прогнозирования. Любые временные ряды, демонстрирующие некоторый паттерн и не являющиеся случайным белым шумом, могут быть смоделированы с помощью модели ARIMA (или её модифицированной версии).

Базовые модели ARIMA задаются тремя членами: p, d, q,

где:

• p – это порядок авторегрессии (AR),
• q – порядок скользящей средней (MA) и
• d – это число дифференцирований, требуемое для того, чтобы сделать временные ряды стационарными (I)

Использование R программы auto.arima из прогностического пакета позволяет выбрать ARIMA-модель, соответствующую информационному критерию Акаике – программа перебирает различные комбинации p, q и d и находит наилучшее соответствие. Здесь мы можем видеть, что программа выбрала порядок авторегрессии 3, порядок скользящей средней 1 и порядок интегрирования 2 (интересно, что auto.arima использует для определения оптимального порядка интегрирования KPSS-тест, уже знакомый тем, кто читал статью о фальсифицировании коэффициента St/F).

Рисунок 6. R программа auto.arima автоматически подобрала наилучшие параметры для ARIMA.

На рисунке 6 мы определили коэффициенты для ARIMA.

Рисунок 7. Степень соответствия статистики для модели, представленной на рисунке 6.

Теперь, наблюдая квадратный корень из среднеквадратической ошибки модели (RMSE) на рисунке 7, мы ожидаем образования небольшой разницы между прогнозируемым и фактическим спросом. На графике, представленном на рисунке 8, прекрасно видно, что эта модель оценивает исторический спрос гораздо точнее, чем OLS.

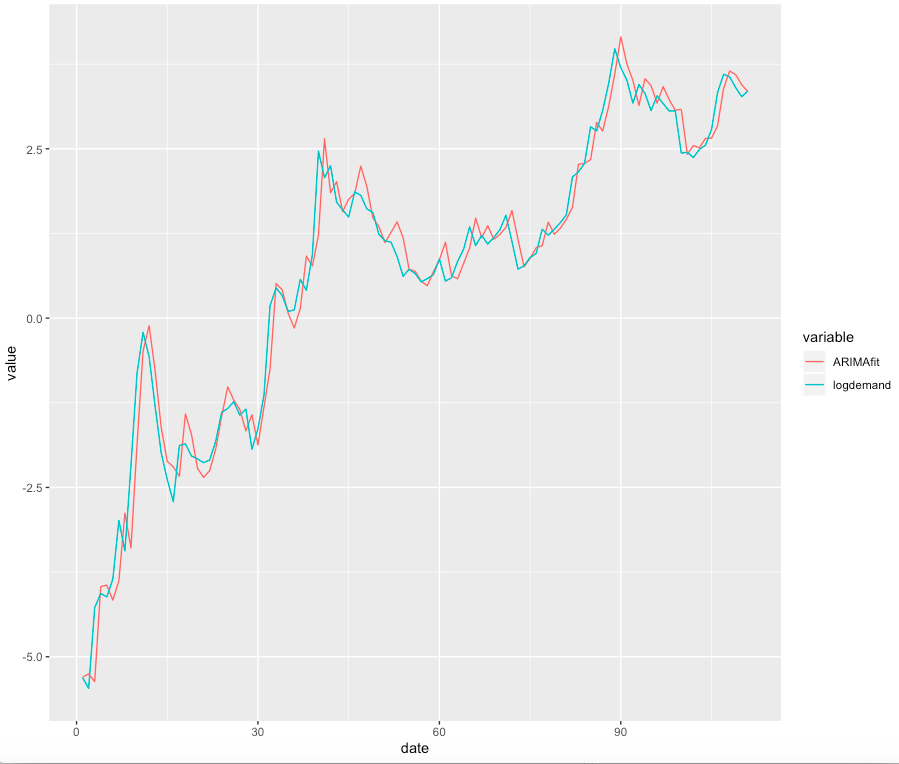Рисунок 8. Расчётные значения ARIMA для логарифмических значений спроса. Уровень соответствия намного выше, чем при использовании метода OLS.

Процесс создания динамического прогноза из ARIMA сложновато выразить здесь в виде формул, но если вам интересно изучить этот вопрос во всех подробностях, то найдите время и ознакомьтесь с этими работами: 1, 2 (англ.).

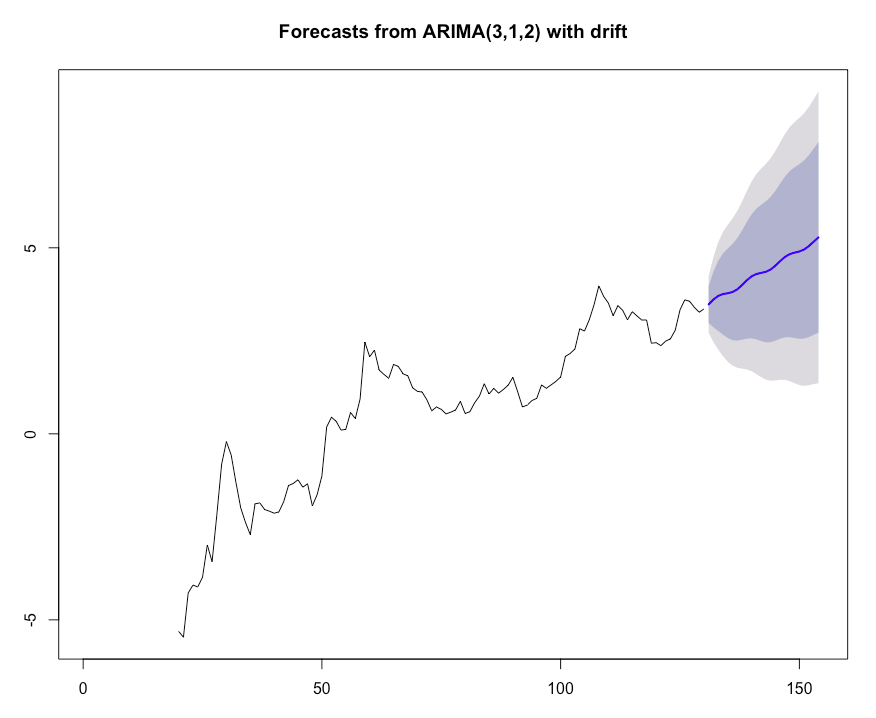Рисунок 9. Прогноз ARIMA для логарифмических значений спроса на следующие 2 года.

Как наш прогноз спроса выглядит на линейной шкале?

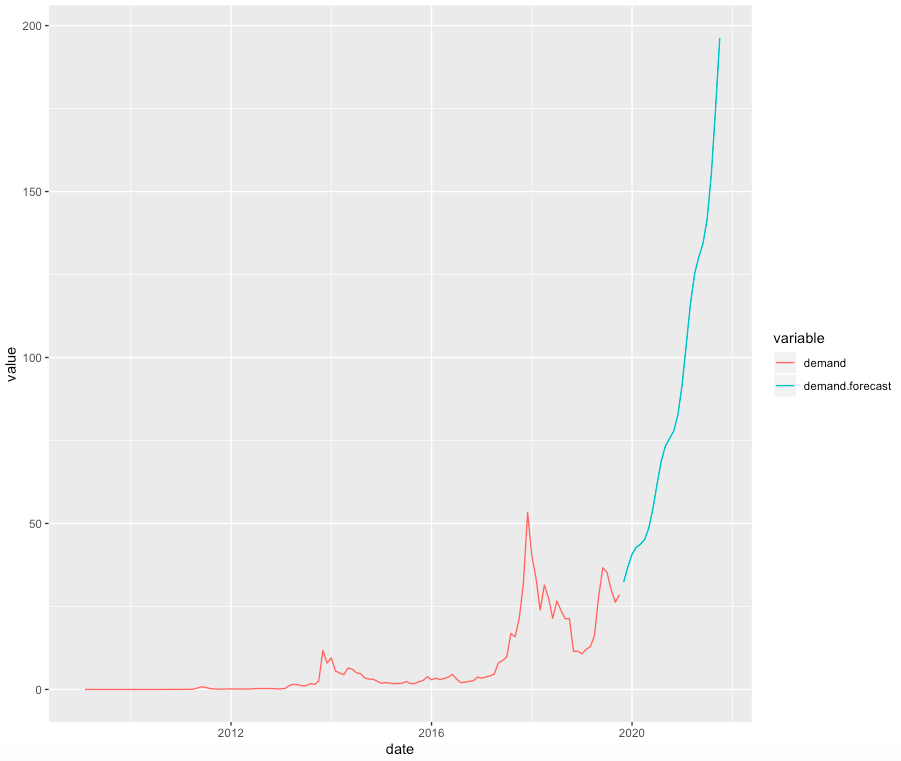Рисунок 10 – прогноз спроса и предложения из ARIMA в линейном пространстве.

Соединение моделей

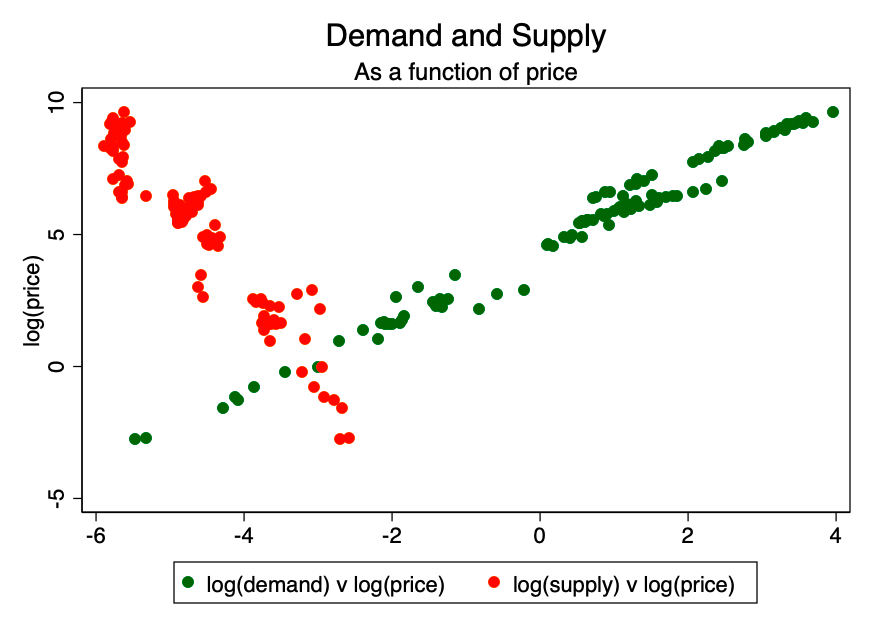Рисунок 11. Спрос и предложение в зависимости от цены.

Теперь мы можем объединить наши прогностические данные и ожидаемые значения запасов и прироста (количества актива) для расчёта прогнозируемой цены.

Ранее мы установили, что P = D/(F/St) см. аксиома 1.

Мы знаем, какими будут (с незначительной погрешностью) прирост и запасы с течением времени, таким образом, мы можем объединить эти цифры и полученный с помощью ARIMA прогноз спроса. Результат показан на рисунке 12.

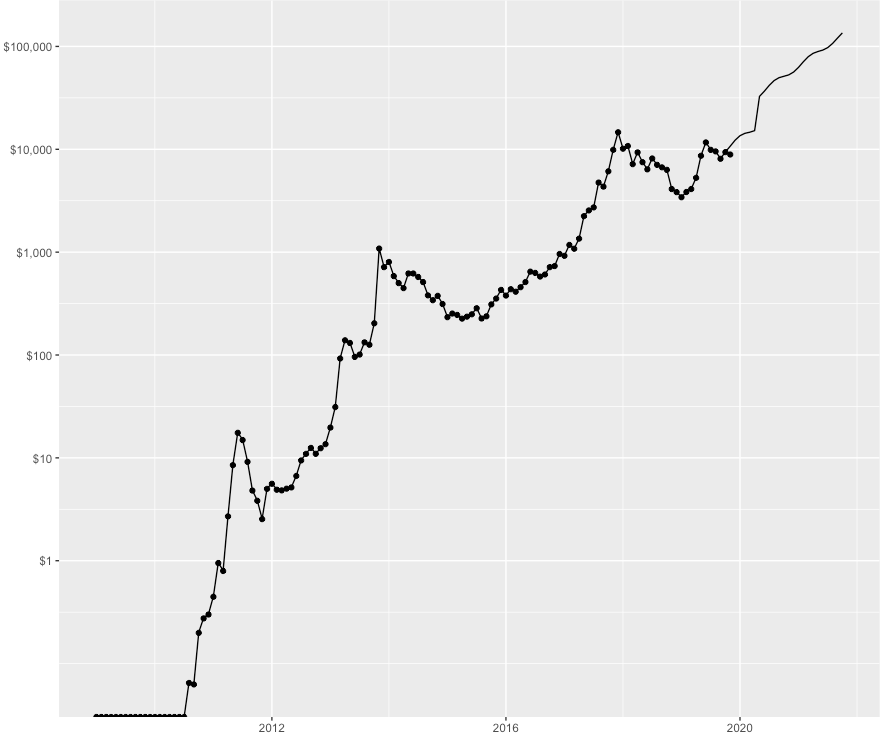Рисунок 12. Фактическая цена отмечена точками, цена модели – линией. Как видно на графике, согласно этой модели, можно ожидать, что цена биткойна превысит 100 000 $ к концу 2021 года.

Заключение

Мы представили простую и относительно лаконичную модель спроса и предложения для цены биткойна, в которой предложение смоделировано исходя из изобилия (то есть от обратного по отношению к дефицитности, определяемой через отношение запасов к приросту). Эта базовая модель обладает потенциалом для расширения, в частности, путём изучения моделей спроса, основанных на других переменных, нежели время.

Предостережения

• Этот прогноз в значительной мере полагается на ARIMA. Расчёты ARIMA могут оказаться неверны – прогностические модели сплошь и рядом оказываются ошибочными. Они являют собой не более чем способ упростить реальность таким образом, чтобы помочь нам лучше её понять. В этой статье мы попытались смоделировать цену биткойна как производное от спроса и предложения.
• Мы не выполняли каких-либо диагностических тестов для проверки ARIMA, и то, насколько доверять представленным результатам, остаётся полностью на усмотрение читателя. Наша цель состояла только в том, чтобы найти способ смоделировать цену как функцию от спроса и предложения, а не найти лучшую модель спроса и предложения. Эта задача остаётся в качестве упражнения для пытливого читателя.
• Кроме того, наша вторая аксиома вполне может оказаться неверна. Время может быть хорошим заменителем для настоящей кривой принятия, однако маловероятно, чтобы им одним можно было объяснить спрос.
• В целом идея о том, что цена является просто функцией от спроса и предложения (т.е. аксиома 1), вполне вероятно, не полностью описывает реальное положение вещей. Вполне могут существовать циклы обратной связи и другие структурные связи (а также эмоциональность потребления и т.п.), никак не учитываемые в этом простом уравнении. Следите за дальнейшим развитием и исследованиями потенциальных структурных отношений.

Подписывайтесь на BitNovosti в Telegram!
Делитесь вашим мнением об этой статье в комментариях ниже.

Оцените материал: