В этой статье автор пытается ответить на вопрос: существует ли взаимосвязь между отношением запасов к приросту (Stock-to-Flow, или S2F) и стоимостью биткойна. Он проверяет предложенную PlanB двойную логарифмическую модель на статистическую достоверность, основываясь на методе наименьших квадратов, на неизменность во времени каждой её переменной и на возможные ложные зависимости. Векторная модель коррекции ошибок (VECM) создана и протестирована на основе исходной модели отношения запасов к приросту. Хотя некоторые из этих моделей с точки зрения информационного критерия Акаике превосходят оригинальную, все они не могут опровергнуть гипотезу о том, что отношение запасов к приросту является важным и неложным предиктором цены биткойна.
Введение
Научный метод сложен для большинства людей. Он контринтуитивен, и поэтому может привести к заключениям, не отражающим мнения авторов. Для того чтобы понять этот метод, необходимо понять и принять его фундаментальную идею: ошибаться нормально. Этому нужно бы учить еще в школе. Если мы будем бояться допустить ошибку, то никогда не сможем предложить ничего нового. История научных открытий полна счастливых случайностей. Случайные находки и открытия могут быть столь же (или даже более) важными, нежели то, над чем они в тот момент работали. Идеи могут быть ошибочными или неубедительными, но то, что обнаруживается в процессе их проверки, создает фундамент для последователей.
По убеждению великого философа науки Карла Поппера, проверка гипотезы на ее ошибочность – это единственный надежный способ добавить веса аргументу о том, что она верна [1]. Если строгие многократные тесты не могут доказать, что гипотеза ошибочна, то с каждым таким тестом вероятность того, что она верна, возрастает. Эта концепция называется фальсифицируемостью (или потенциальной опровержимостью) теории. В этой статье я попытаюсь сфальсифицировать модель определения цены биткойна на основе коэффициента Stock-to-Flow, описанную в статье PlanB «Моделирование цены биткойна исходя из его дефицитности» [2].
Определение проблемы
Чтобы сфальсифицировать гипотезу, нужно сначала установить, в чем она состоит:
Нулевая гипотеза (H0): стоимость биткойна является функцией от его коэффициента Stock-to-Flow
Альтернативная гипотеза (H1): стоимость биткойна не является функцией от его коэффициента Stock-to-Flow
PlanB в своей статье [2] решил проверить H0, соотнеся регрессию обычных наименьших квадратов (OLS) на натуральном логарифме рыночной капитализации Биткойна и натуральном логарифме коэффициента Stock-to-Flow. Автор не представил ни сопутствующей диагностики, ни какой-либо определенной причины для логарифмического преобразования обеих переменных, кроме идеи о том, что двойную логарифмическую модель можно выразить в виде степенной зависимости. Будучи нестационарной, эта модель не учитывает возможность установления ложных зависимостей.
Метод
В сегодняшней статье мы рассмотрим эту модель, проведем диагностику нормальной регрессии и определим, было ли преобразование логарифма необходимо или целесообразно (или и то, и другое), а также исследуем возможные вмешивающиеся факторы (конфаундеры), взаимодействия и чувствительность.
Еще одна проблема, которую мы исследуем, – это проблема нестационарности. Стационарность (неизменность во времени) является необходимым условием большинства статистических моделей. Имеется в виду идея о том, что, если тренд относительно времени отсутствует в средних значениях (или дисперсии), то он отсутствует и в любой момент времени.
Помимо анализа стационарности, мы исследуем также возможность коинтеграции.
Условные обозначения
Традиционно расчетное значение статистического параметра обозначается «шапкой» над символом. Здесь вместо него мы будем использовать [ ], т.е. расчетное значение β = [β]. Матрицу 4×4 мы будем представлять как [r1c1, r1c2 \ r2c1, r2c2] и т.д. Для обозначения индексированных элементов будем использовать символ @ – например, для 10-й позиции в векторе X обычно используется X с подстрочным индексом 10. Вместо этого, мы будем писать X@10.
Обычные наименьшие квадраты (OLS)
Регрессия обычных наименьших квадратов – это метод нахождения линейной зависимости между двумя и более переменными.
Для начала давайте определим линейную модель как некоторую функцию X, которая равна Y с некоторой погрешностью.
Y = βX+ε
где Y – зависимая переменная, X – независимая переменная, ε – это величина погрешности, а β – множитель X. Задача OLS – вывести значение β так, чтобы минимизировать ε.
Для того чтобы вывести надежное расчетное значение [β], необходимо соблюсти некоторые основные условия:
Линейность
Начнем с рассмотрения не преобразованного в диаграмму рассеяния отношения рыночной капитализации и коэффициента S2F (данные из источника [4]).
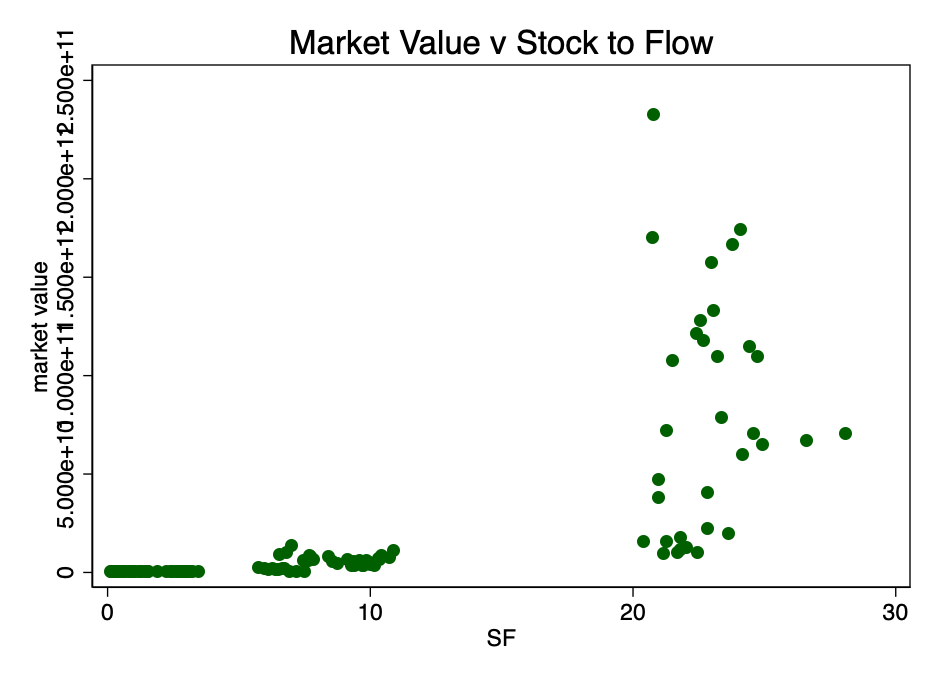Рис. 1 – Отношение рыночной капитализации к коэффициенту Stock-to-Flow. Данные слишком скудны, чтобы можно было установить взаимосвязь. На рисунке 1 ясно видна достаточная причина для взятия логарифма рыночной стоимости: разброс значений слишком велик. При взятии логарифма от рыночной стоимости (но не S2F) и повторном построении диаграммы мы получаем знакомый паттерн (рисунок 2).
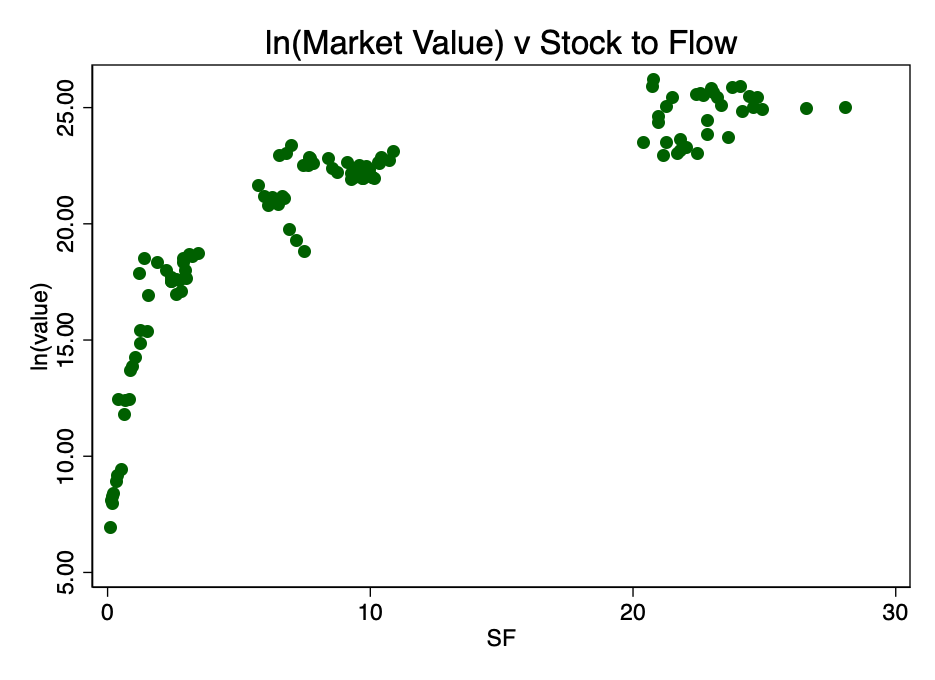Рис. 2 – отношение логарифма рыночной капитализации и коэффициента S2F. Возникает отчетливый логарифмический паттерн. Взяв логарифм от коэффициента S2F и построив диаграмму уже с ним, мы получаем очевидный линейный паттерн, идентифицированный автором источника [2] (PlanB) на рисунке 3.
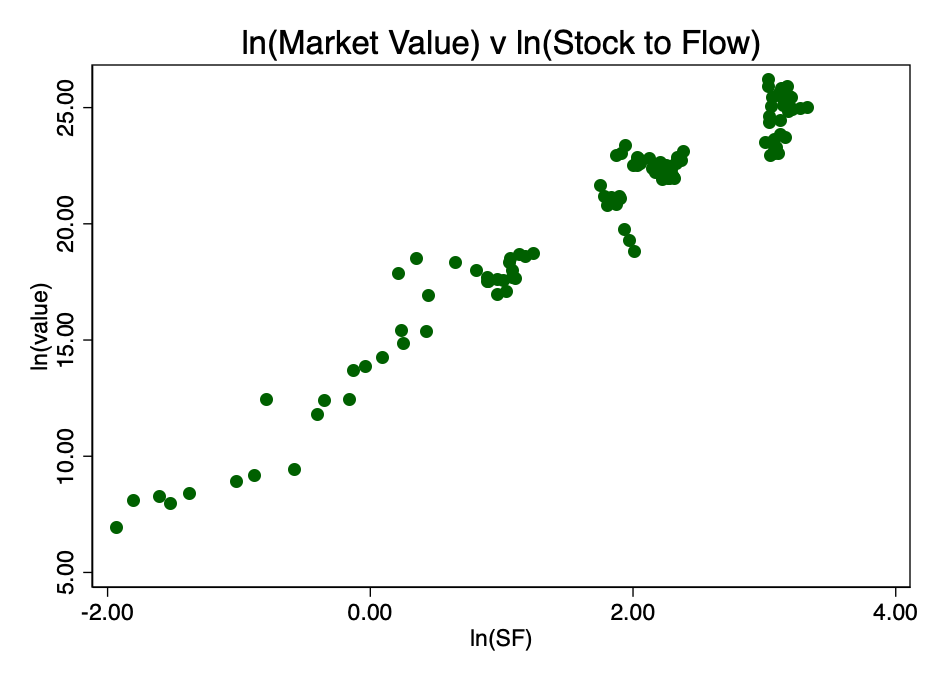Рис. 3 – отношение логарифмов рыночной капитализации и коэффициента S2F. Возникает очевидная линейная зависимость. Это подтверждает правильность выбора двойного логарифма как единственного варианта, дающего в результате хорошо просматриваемую линейную зависимость.
Альтернативным вариантом преобразования было нахождение квадратного корня из обоих параметров. Получаемый при этом паттерн показан на рисунке 4.
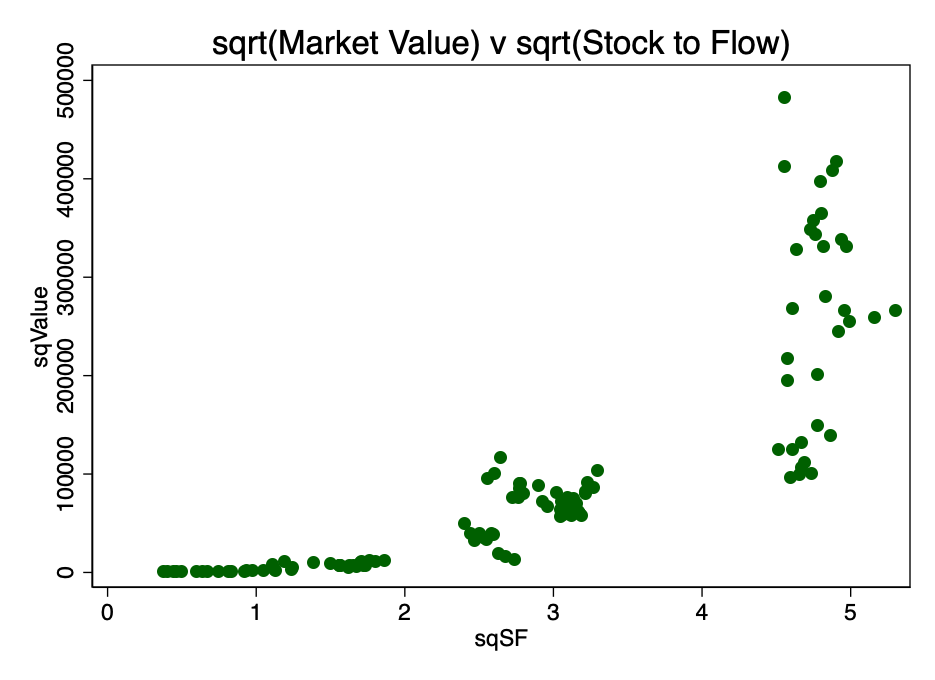Рис. 4 – результат преобразования путем вычисления квадратного корня из рыночной капитализации и коэффициента S2F. Очевидно, что двойное логарифмирование является наиболее подходящим преобразованием для удовлетворения первого условия, линейности.
Таким образом, предварительный анализ не опровергает H0.
Результаты двойной логарифмической регрессии приведены на рисунке 5 ниже, где [β] = [3,4, 3,7] (доверительный интервал 95%).
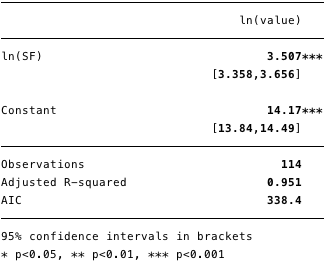Рис. 5 – результаты для двойной логарифмической регрессии. Используя эту модель, мы теперь можем определить остатки [ε] и расчетные значения [Y], а также проверить соответствие другим условиям.
Гомоскедастичность
При соблюдении условия о постоянстве дисперсии в величине погрешности (т.е. о гомоскедастичности), погрешность для каждого значения прогнозируемой стоимости колеблется произвольным образом около нуля. Следовательно, график отношения остаточной стоимости к расчетной (рис. 6) представляет собой простой, но эффективный способ графически проверить выполнение этого условия. На рисунке 6 присутствует некоторый паттерн, а не случайное рассеяние, что указывает на непостоянство дисперсии в величине погрешности (т.е. на гетероскедастичность).
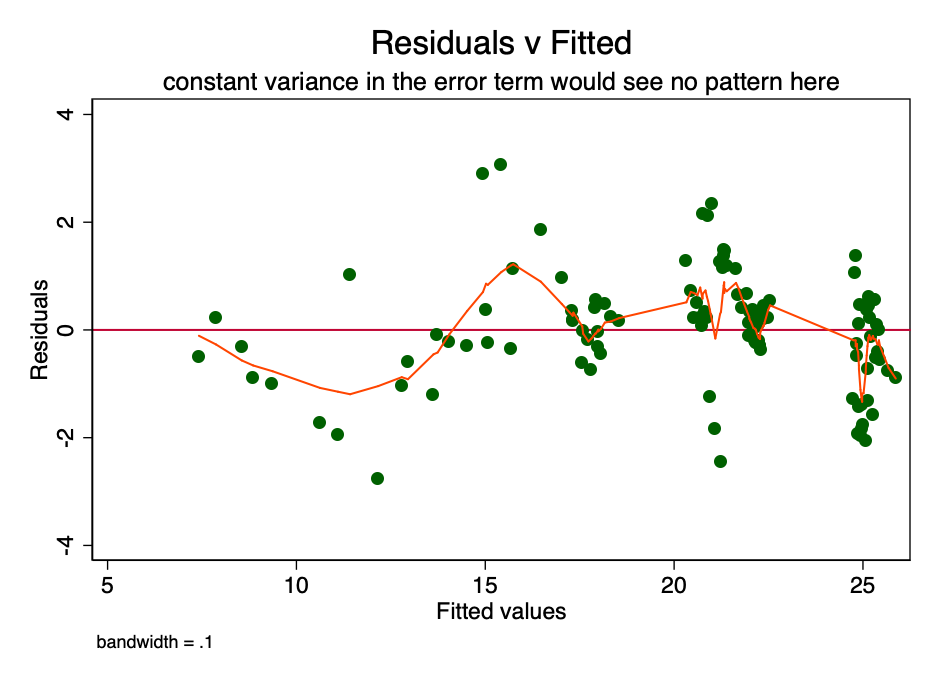Рис. 6 – график отношения остаточной стоимости к расчетной. При постоянной дисперсии погрешности, паттерна не наблюдалось бы. Наличие паттерна указывает на возможную проблему. Следствием подобной гетероскедастичности является бóльшая дисперсия и, соответственно, меньшая точность расчетных значений коэффициентов [β]. Кроме того, она приводит к большей, чем следует, значимости p-значений, поскольку метод OLS не выявляет повышенную дисперсию. Поэтому для расчета t- и F-величин мы используем заниженное значение дисперсии, приводящее к более высокой значимости. Это влияет также на 95% доверительный интервал для [β], который тоже является функцией дисперсии (через стандартную погрешность).
На этом этапе можно безопасно продолжать регрессию, отдавая себе отчет в существовании этих проблем. Способы справиться с ними существуют – например, взятие бутстреп-выборок или робастная оценка дисперсии.
Рис. 7 — Влияние гетероскедастичности показано в робастном оценивании. Как видно на рисунке 7, несмотря на небольшое увеличение дисперсии (см. расширенный доверительный интервал), по большому счету, присутствующая гетероскедастичность в действительности не оказывает настолько пагубного воздействия.
На данном этапе мы не можем опровергнуть H0 по причине гетероскедастичности.
Нормальное распределение ошибок
Удовлетворение условия о том, что погрешность в норме распределяется со средним значением, равным нулю, не так важно, как удовлетворение условий о линейности или гомоскедастичности. При не соответствующих нормальному распределению, но не искаженных остатках, доверительные интервалы будут чрезмерно оптимистичными. Если же остатки искажены, то искажен может быть и конечный результат. Однако, как видно из рисунков 8 и 9, остатки находятся в пределах нормы. Среднее значение, как кажется, примерно равно нулю, и хотя формальный тест, вероятно, опроверг бы гипотезу о нормальном распределении, остатки соответствуют кривой нормального распределения в достаточной мере, чтобы доверительные интервалы не были затронуты.
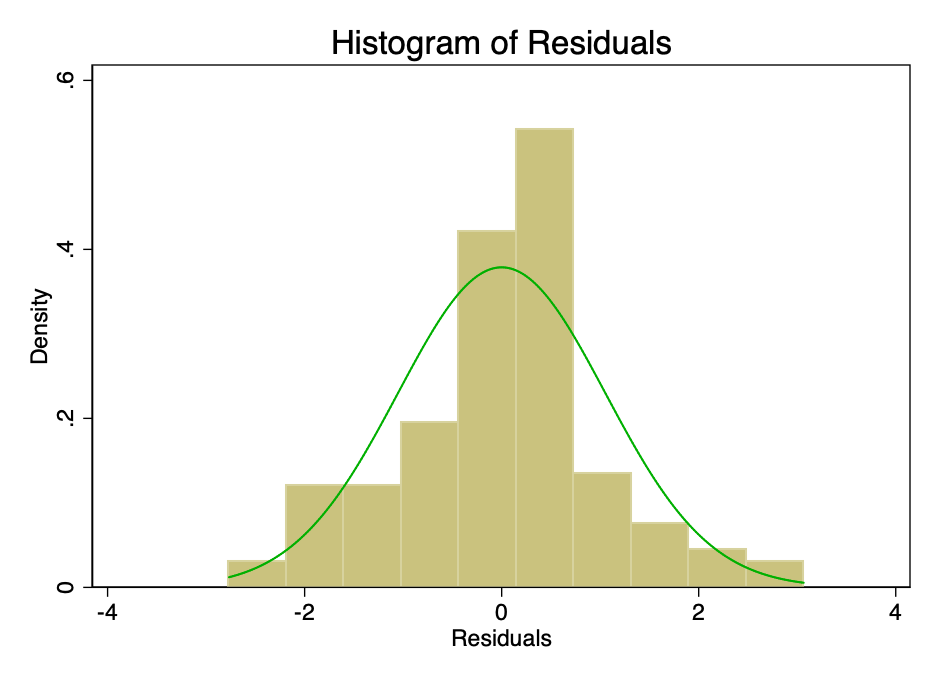Рис. 8 – гистограмма погрешности с наложенной на нее (зеленой) кривой нормального распределения. 
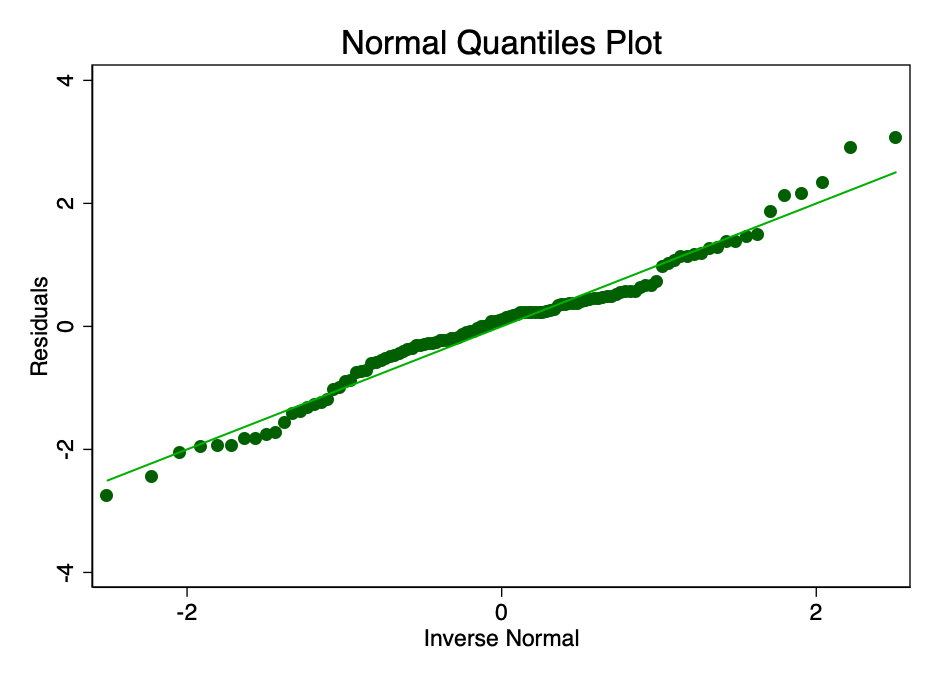Рис. 9 – график с нормальными квантилями величины погрешности. Чем ближе точки к линии, тем лучше нормальная подгонка. Сила воздействия (леверидж)
Леверидж здесь – это концепция, согласно которой не все точки данных в регрессии вносят равный вклад в оценку коэффициентов. Некоторые точки с высокой силой воздействия могут существенно изменить коэффициент в зависимости от того, присутствуют они или нет. На рисунке 10 ясно видно, что на ранних этапах (март, апрель и май 2010 г.) есть несколько внушающих сомнение моментов. В этом нет ничего удивительного и PlanB в своей статье [2] упоминал о том, что сбор данных за ранний период был сопряжен с определенными трудностями.
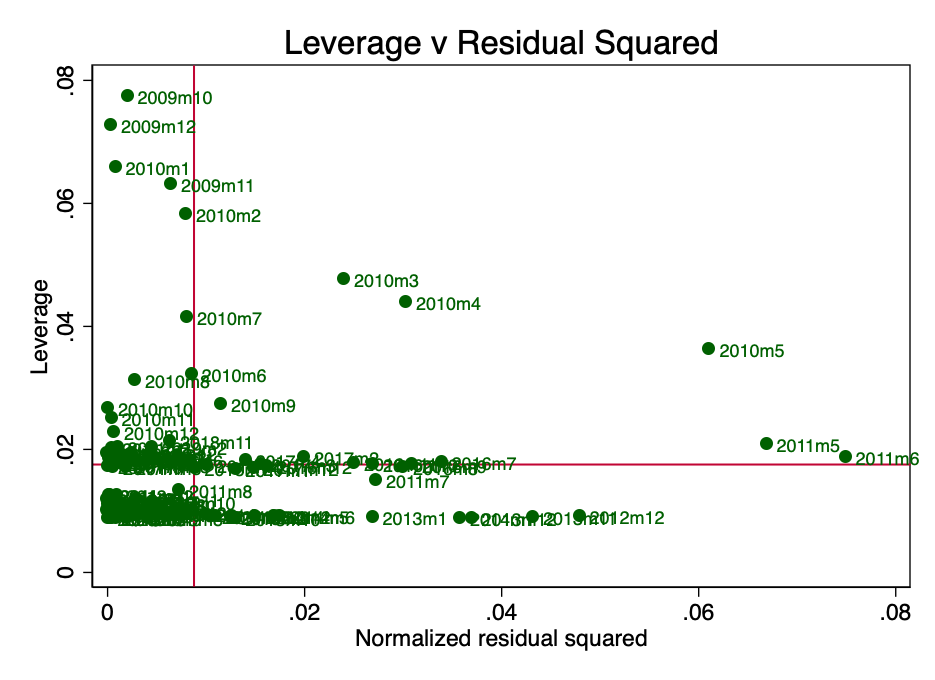Рис. 10 – сила воздействия и возведенные в квадрат нормализованные остатки. Если мы повторно запускаем регрессию без этих точек (предположим, что в них есть какая-то ошибка), то, поскольку мы знаем о проблеме гетероскедастичности, нам нужно использовать робастные оценки.
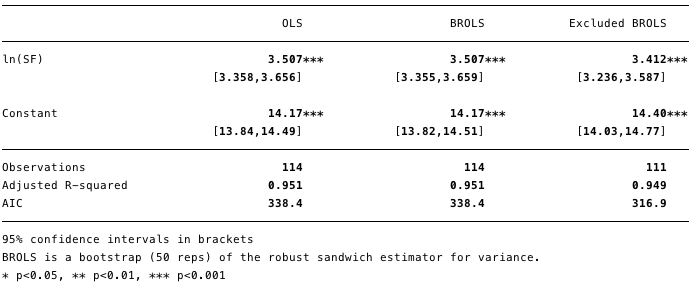Рис. 11 – удаление точек с высокой силой воздействия существенно изменило расчетное значение [β] и улучшило значение информационного критерия Акаике (AIC).На рисунке 11 видно, что удаление этих удаление этих трех точек значительно изменяет расчетное [β] и значение информационного критерия Акаике значительно снижается, что говорит о том, что модель является лучшей, несмотря на более низкий R².
Резюме по OLS
Базовая диагностика указывает на несколько небольших и устранимых проблем с исходными наименьшими квадратами. На этом этапе мы не можем опровергнуть H0.
Стационарность
Стационарным называют процесс с общим порядком 0 (напр., I(0)). Нестационарный процесс – это I(1) и более. Вычисление интеграла в этом контексте – это скорее «для бедных», сумма разностей со сдвигом по времени. I(1) означает, что при вычитании первого лага из каждого значения в серии получается I(0) процесс. Довольно хорошо известно, что регрессия по нестационарным временным рядам может привести к выявлению ложных связей.
На рисунках 12 и 13 ниже видно, что мы не можем опровергнуть нулевую гипотезу расширенного теста Дики-Фуллера (ADF). Нулевая гипотеза ADF-теста заключается в том, что данные являются нестационарными, то есть нельзя утверждать, что данные стационарны.
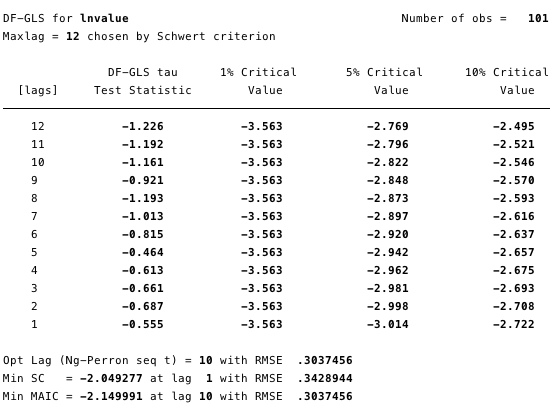Рис. 12 – расширенный тест Дики-Фуллера для единичного корня на ln(стоимость). 
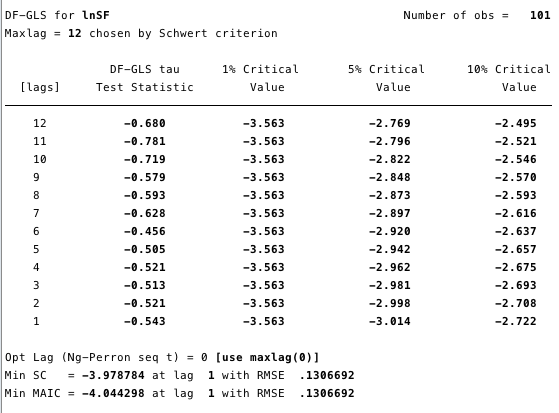Рис. 13 – расширенный тест Дики-Фуллера для единичного корня на ln(S2F). Критерий Квятковского-Филлипса-Шмидта-Шина (KPSS) – это дополнительный тест на стационарность к тестам ADF. Нулевая гипотеза KPSS состоит в том, что данные являются стационарными. Как видно на рисунках 14 и 15, мы можем опровергнуть стационарность для большинства лагов в обеих переменных.
Рис. 14 и 15 – KPSS-тест против нулевой гипотезы о стационарности. KPSS-тесты доказывают, что эти две серии, вне всякого сомнения, являются нестационарными. И в этом есть некоторая проблема. Если серия не является стационарной по меньшей мере относительно тренда, то метод OLS может идентифицировать ложные зависимости. Единственное, что мы могли сделать – это взять разницу между логарифмом и месячным значением каждой переменной и перестроить наши наименьшие квадраты. Однако, благодаря тому, что этот вопрос довольно широко распространен в эконометрических кругах, у нас есть гораздо более надежный фреймворк, называемый коинтеграцией.
Коинтеграция
Коинтеграция – это способ разобраться с парой (или более) процессов I(1) и определить, есть ли между ними взаимосвязь и в чем она состоит. В качестве наглядной иллюстрации коинтеграции часто приводится упрощенный пример пьяницы и его собаки [3]. Представьте себе пьяного человека, направляющегося домой, выгуливая на поводке собаку. Пьяницу совершенно непредсказуемым образом шатает по всей ширине дороги. Собака двигается тоже довольно сумбурно: обнюхивает деревья, лает, что-то роет лапами – такая беспокойная собачонка. Однако радиус движения собаки будет ограничен длиной поводка, удерживаемого пьяницей. То есть можно утверждать, что в любой точке маршрута пьяницы собака будет находиться в пределах длины поводка от него. (Конечно, мы не можем предсказать, в каком направлении от пьяницы она будет находиться в каждый момент времени, но она будет в пределах поводка.) Это очень упрощенная метафора коинтеграции – собака и ее хозяин двигаются вместе.
Сравните это с корреляцией: скажем, бродячая собака следует за собачонкой пьяницы на протяжении 95% их пути, а затем убегает с лаем в другую сторону за проехавшим мимо автомобилем. Корреляция между маршрутами бродячей собаки и пьяницы была бы очень сильной (буквально R²: 95%), однако, как и многие случайные связи пьяницы, это отношение ровным счетом ничего бы не значило – его нельзя использовать для прогнозирования местонахождения пьяницы, поскольку для какого-то фрагмента пути прогноз на основе этих данных окажется верным, но для некоторых частей он будет совершенно неточным.
Для того чтобы найти местоположение пьяницы, сначала мы должны понять, какую спецификацию порядка запаздывания следует использовать в нашей модели.
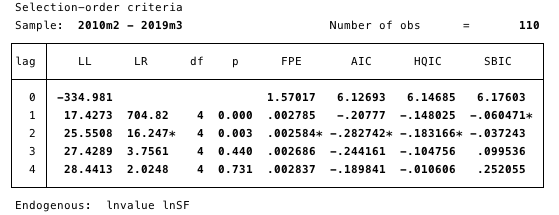Рис. 16 – спецификация порядка запаздывания. Минимальное значение AIC, используемое для определения. Здесь мы определяем наиболее подходящий для исследования порядок запаздывания через выбор минимального значения AIC порядка 2.
Далее нам нужно определить наличие коинтегрирующего отношения. Фреймворк Йохансена [5, 6, 7] дает нам для этого превосходный инструментарий.
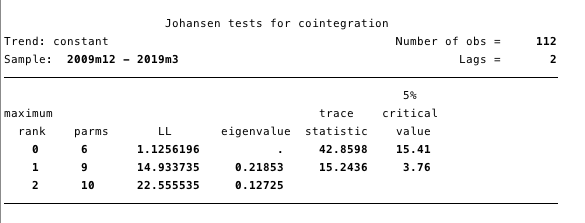Рис. 17 – тест Йохансена на коинтеграцию. Результаты, представленные на рисунке 17, дают нам основания утверждать, что между ln(стоимость) и ln(S2F) есть по меньшей мере одно коинтегрирующее уравнение.
Мы определяем нашу VECM как:
Δy@t =αβ`y@t-1+Σ(Γ@iΔy@t-1)+v+δt+ε@t
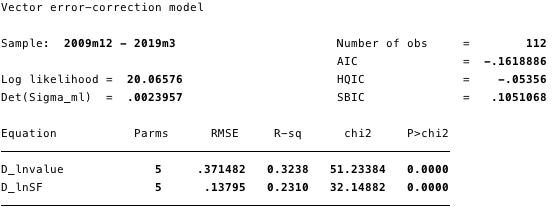Рис. 18 – информация обо всех уравнениях модели. 
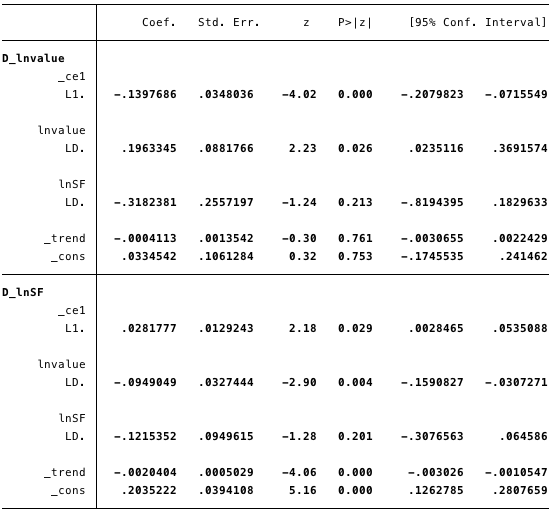Рис. 19 – расчетные значения краткосрочных параметров и их статистика. 
Рис. 20 — коинтегрирующее уравнение для модели. 
Рис. 21 – информационный критерий Акаике для VECM. На рисунках выше мы имеем следующие расчетные значения:
- [α] = [-0,14, 0,03]
- [β] = [1, -4,31],
- [v] = [0,03, 0,2] и
- [Γ] = [0,196, -0,095 \ -0,318, -0,122].
В целом результат указывает на то, что модель подходит хорошо. Коэффициент ln(S2F) в коинтеграционном уравнении является статистически значимым, равно как и параметры корректировки. Параметры корректировки указывают на то, что, если прогнозы из коинтеграционного уравнения являются положительными, то ln(стоимость) находится ниже своего равновесного значения, поскольку коэффициент на ln(стоимость) в коинтеграционном уравнении отрицателен. Расчетное значение коэффициента [D ln(стоимость)]L. ce1 составляет -0,14.
Таким образом, если стоимость биткойна слишком мала, она быстро поднимается обратно до уровня соответствия ln(S2F). Расчетный коэффициент [D ln(S2F)] L. ce1, равный 0,028, подразумевает, что при слишком низкой стоимости биткойна он корректируется до равновесного уровня.
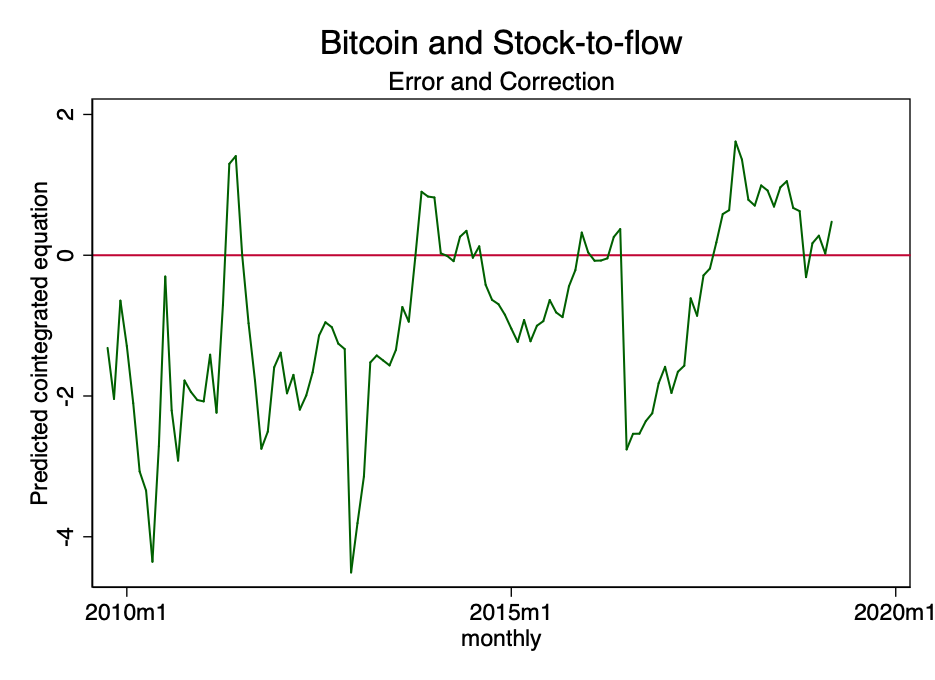Рис. 22 – прогнозируемое коинтеграционное уравнение. На рисунке выше видно, что результат коинтеграционного уравнения имеет тенденцию стремиться к нулю. Хотя формально оно может быть и нестационарным, оно определенно стремится к стационарности.
Из пользовательского руководства ПО Stata:
Сопровождающая матрица для VECM с K эндогенных (внутрисистемных) переменных и r коинтеграционных уравнений имеет Kr собственных значений. Если процесс стабилен, то модули остальных собственных значений r составляют строго меньше одного. Поскольку общего распределения для модулей собственных значений нет, определить, являются ли они слишком близкими к единице, может быть трудно.
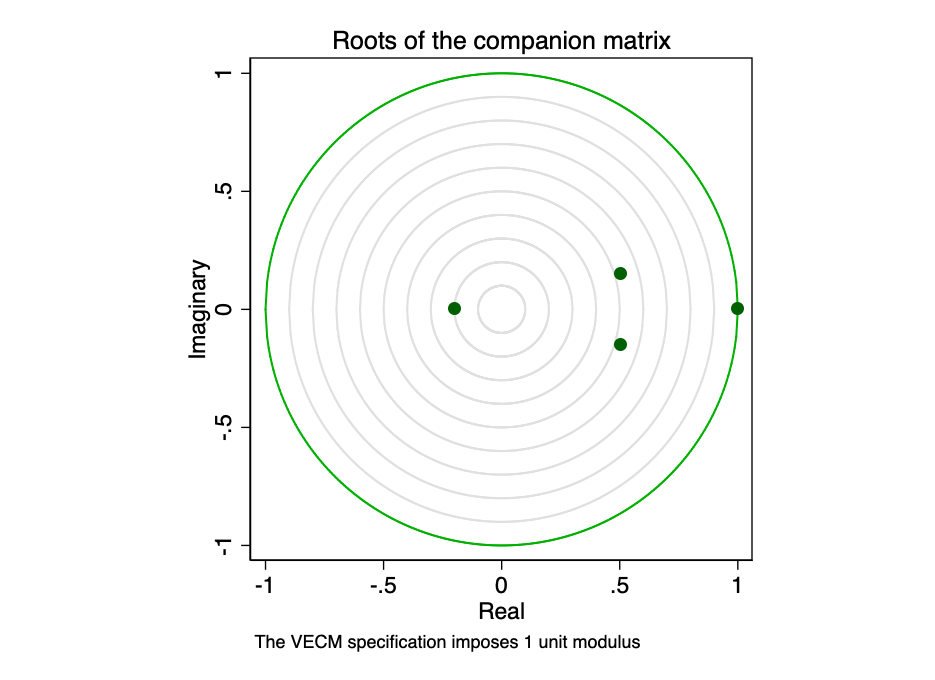Рис. 23 – корни сопровождающей матрицы. Графическое изображение собственных значений показывает, что ни одно из оставшихся собственных значений не находится близко к краю единичной окружности. Проверка устойчивости нашей модели не указывает на ее ошибочность.
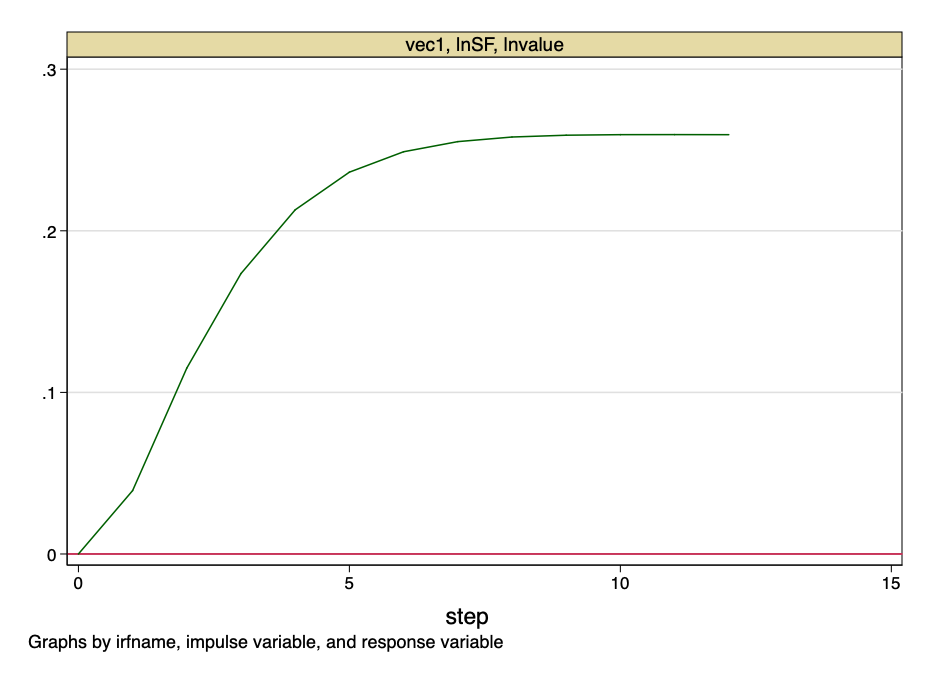Рис. 24 – функция импульсного отклика. Приведенный выше рисунок указывает на то, что ортогонализованный скачок к значению коэффициента S2F оказывает постоянное влияние на стоимость биткойна.
И в этом месте мы подведем черту. Отношение запасов к приросту не является случайной величиной. Это функция с известным значением во времени. Никаких скачков значений S2F не будет – его стоимость может быть с точностью рассчитана заранее. Однако эта модель дает очень убедительные доказательства того, что существует фундаментальная неложная зависимость между значением коэффициента S2F и стоимостью биткойна.
Ограничения
В этом исследовании мы не учитывали каких-либо вмешивающихся факторов (конфаундеров). С учетом приведенных выше доказательств, маловероятно, чтобы какие-либо конфаундеры могли оказать существенное влияние на наше заключение – мы не можем опровергнуть H0. Мы не можем утверждать, что никакой зависимости между отношением запасов к приросту и стоимостью биткойна нет. Если бы это было так, не было бы коинтеграционного уравнения.
Заключение
Хотя некоторые из представленных здесь моделей с точки зрения информационного критерия Акаике превосходят оригинальную модель PlanB, все они не могут опровергнуть гипотезу о том, что отношение запасов к приросту является важным и неложным предиктором цены биткойна.
Для иллюстрации, вернемся к метафоре с пьяницей из примера выше: если сравнить стоимость биткойна с пьяницей, то коэффициент Stock-to-Flow – это не собака, которую он ведет на поводке, но скорее дорога, по которой он идет. Пьяницу будет шатать по всей ширине дороги, иногда он будет поскальзываться, пропускать повороты или даже срезать какие-то углы, но в целом он будет придерживаться дороги домой.
То есть, вкратце, биткойн – это пьяница, а отношение запасов к приросту – это дорога, по которой он идет.
Цитируемые материалы
Примечания:
- Для всех анализов использовалось ПО Stata 14.
- Статья не содержит финансовых рекомендаций.
Подписывайтесь на BitNovosti в Telegram!
Делитесь вашим мнением об этой статье в комментариях ниже.
